August 12th, 2012 .
One of the things I’ve been wanting to investigate more since rendering clouds on Happy Feet 2 is using more physically based phase functions for volume lighting. The volume phase function describes the direction of scattered light relative to the incoming light’s direction – either isotropic (scattering light evenly in all directions), or anisotropic – scattering mostly forward, or mostly back, or some more complicated distribution altogether. Many volumes, such as smoke, are generally pretty isotropic, but clouds have quite a particular scattering behaviour, determined by the size, and distribution of microscopic water droplets that comprise their form. On HF2 we used a combination of two henyey-greenstein distributions, which was good enough for the task at hand, but after spending so long back then researching atmospheric optics, I’ve been curious to try something more realistic.
Antoine Bouthors’ excellent Phd thesis, Realistic rendering of clouds in realtime, spends a few pages on the Mie phase function – a good fit for many types of clouds. Clouds are highly anisotropic – at each scattering event, over 90% of the energy gets scattered in roughly the same direction that it enters (the strong forward peak), which is what gives the characteristic ‘silver lining’ when looking through a cloud towards the sun. Of the remaining energy scattered in other directions, diffraction and interference create some interesting optical effects such as the fogbow, or glory.
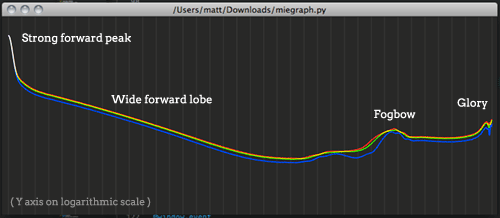
As part of Antoine’s work, he used Mieplot to generate scattering data for a general purpose droplet size distribution found in clouds, and published the data online – the relevant files are Mie0.txt and MiePF3.txt. The scattering distributions are divided into two to make it easier to sample – I imagine because the forward peak is so strong, attempting to importance sample it would barely leave any samples in the sideways or backward directions, so it helps to sample the rest of the function independently from the peak, and combine with weighted probabilities. In a traditional lighting pipeline where the phase function is just being used to weight lighting contribution and not sample new scattering vectors, we can ignore this and combine the data into a single set. To verify the results I wrote a little python script using pyglet to add the split data together and graph them on a log scale, as in the thesis – It’s pleasing to see it matches up perfectly. I also normalised the data to sum to 1.0 over the RGB channels.
For rendering in Houdini, the original plan was to copy the data in as a VEX array, and lookup/interpolate the data based on the input angle, but I think I may have hit a limit to the size of arrays VEX lets you define – arrays of a handful of float items worked fine, but using the full 1800 values introduced compilation errors. So as a more portable alternative, I brought the data into blender to generate an 1800 x 1 pixel OpenEXR image containing the scattering values. This is a lot more convenient to look up, and is easy to then reuse in a renderman shader for example. To sample the image using the U coordinate, the angle between light direction and eye direction needs to be fit to a 0-1 range. This is trivial to do in VOPs, replicating:
U = acos(normalize(I) . normalize(L)) / pi … and feeding that into a color map node.
You can download the EXR file here: mie_phase_function.exr
and hip file: cloudphase2.hipnc.zip
Because this phase function is so heavily forward scattering, by default the volume may seem dark from any other angle than directly in front of the light. For best results:
- Set up your scene to be more physically plausible, with a high dynamic range in lighting, viewed through a tone mapping transform (or at least a gamma curve). This way, with enough intensity in your main light, you’ll be able to see the backward and sideways scattered light, even though the light in the strong forward peak will be very intense. The tone mapping should bring the peak back into a more acceptable range while still leaving the other angles visible.
- Render some form of multiple scattering additional to the single scattering, to fill out the overall light in the volume. This can be faked in any number of ways – in Houdini one way could be to add in an additional weak isotropic phase function (higher orders of scattering tend towards isotropic scattering after light has bounced around randomly for a while), perhaps with a blurry deep shadow map, or however you like to fake multiple scattering effects. Even adding in a constant ambient term can help substantially.